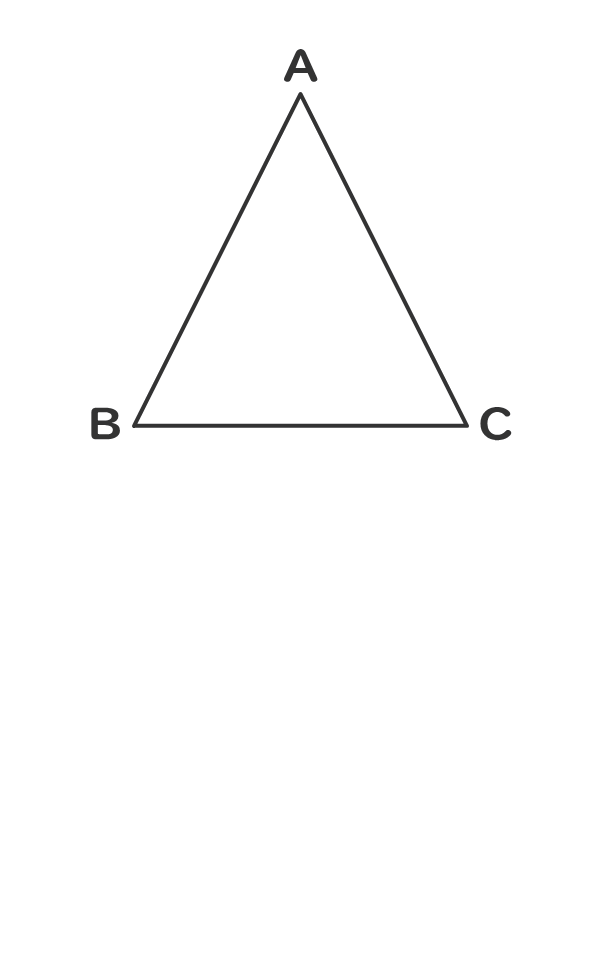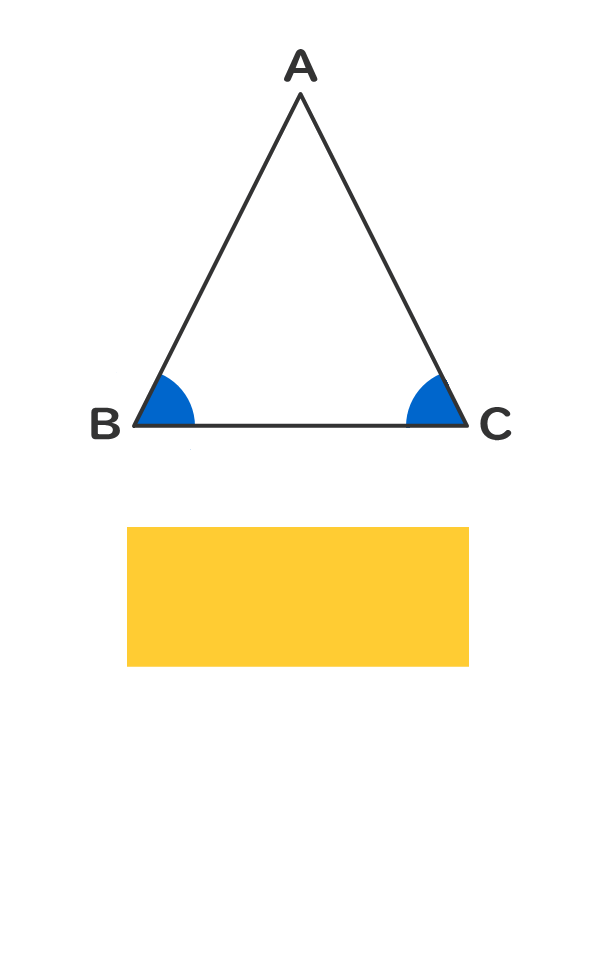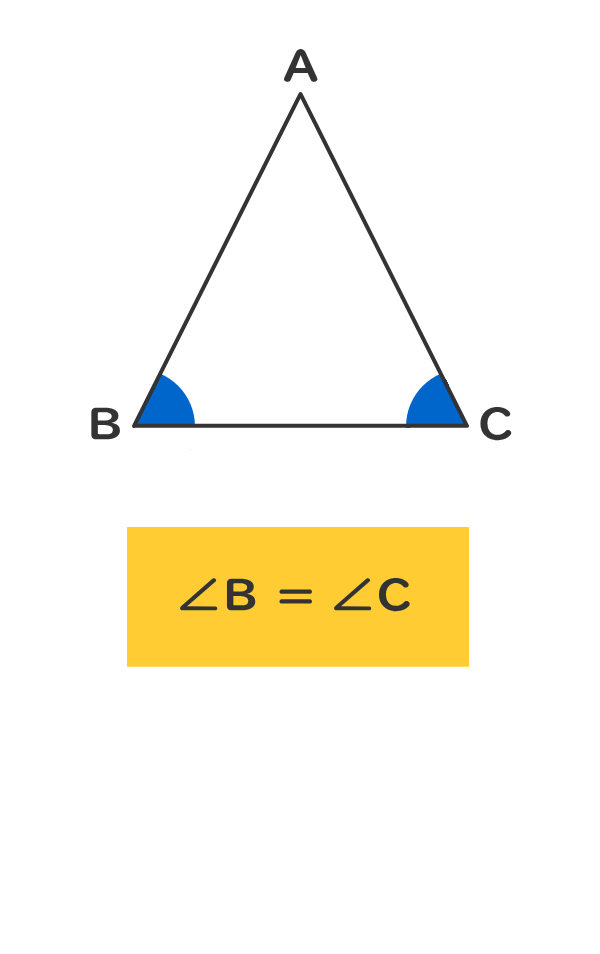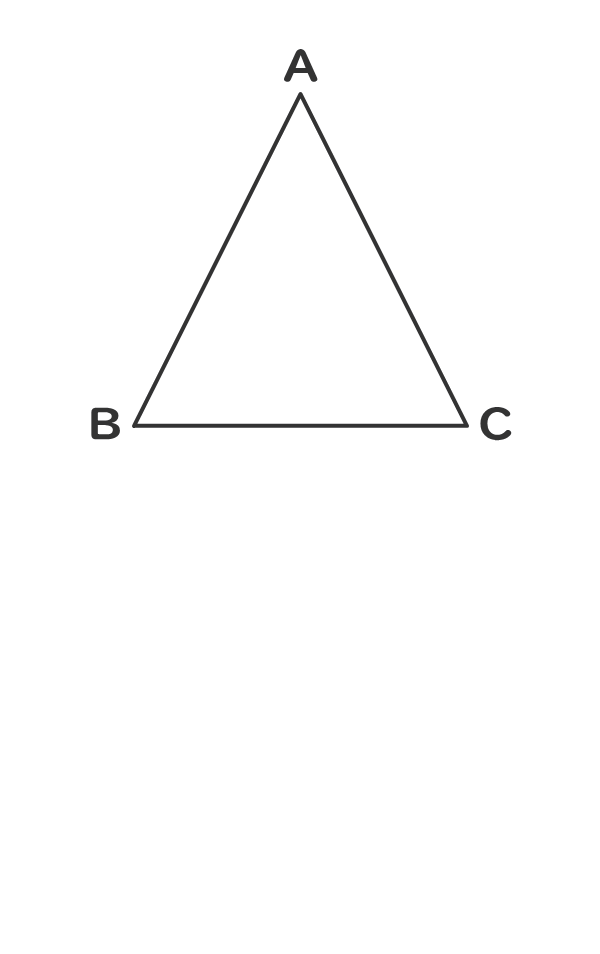
二等辺三角形(にとうへんさんかくけい、英 isosceles triangle )は、三角形の一種で、3 本の辺のうち(少なくとも)2 本の辺の長さが等しい図形である。 長さの等しい 2 辺を等辺といい、残りの 1 辺を底辺とよぶ。2 本の等辺が共有する頂点をとくに二等辺三角形の頂点という。
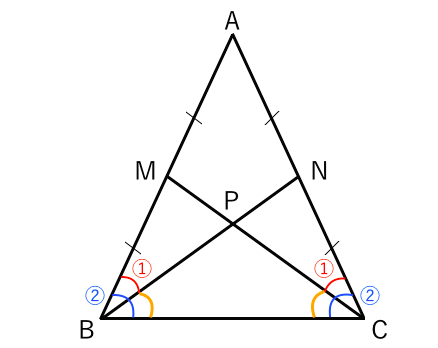
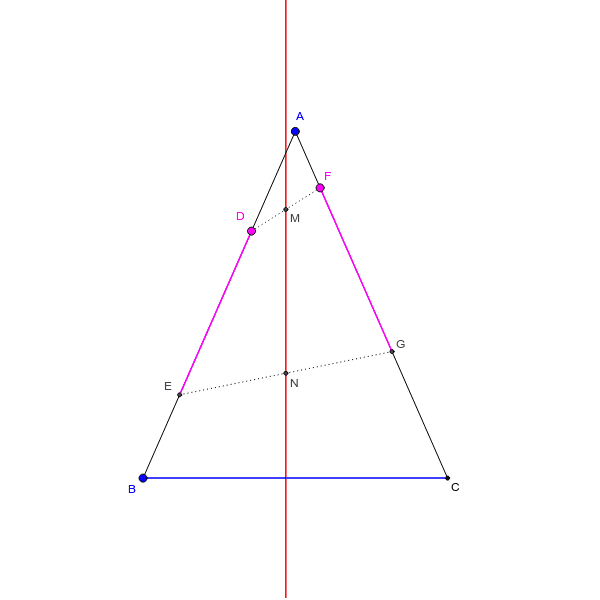
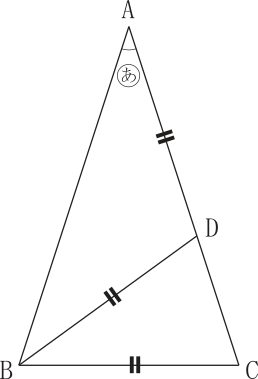
二 等辺 三角形 比-ここまでで、線分比について次の3つのヒントが集まったね。 ① aq:qc=ab:cb ② ap:pb=ac:bc ③ ap:pb=aq:qc つなげて考えると、 ab:cb=ac:bc となるね。ここで、bcは共通だから、 ab=ac が言える。つまり、 abcの正体は 「ab=acの二等辺三角形」 なんだ。三角形と比の定理 したがって efgは二等辺三角形となる。 確認 四角形abcdで、p,rはそれぞれ辺ad, bcの中点、q,sはそれぞれ対角線bd,acの中点である。 答表示 a b
二 等辺 三角形 比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「二 等辺 三角形 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  | |
「二 等辺 三角形 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「二 等辺 三角形 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「二 等辺 三角形 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「二 等辺 三角形 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「二 等辺 三角形 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  |  |
「二 等辺 三角形 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「二 等辺 三角形 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 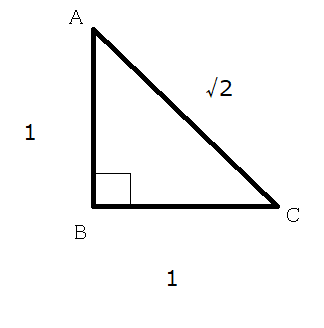 |
 | 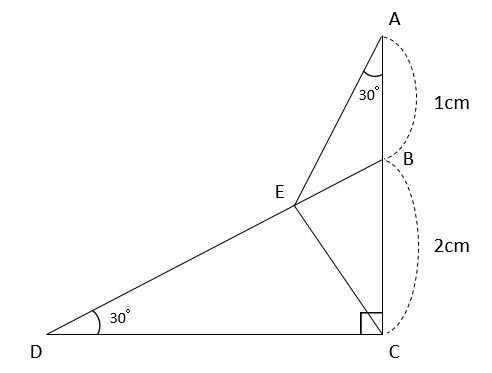 |
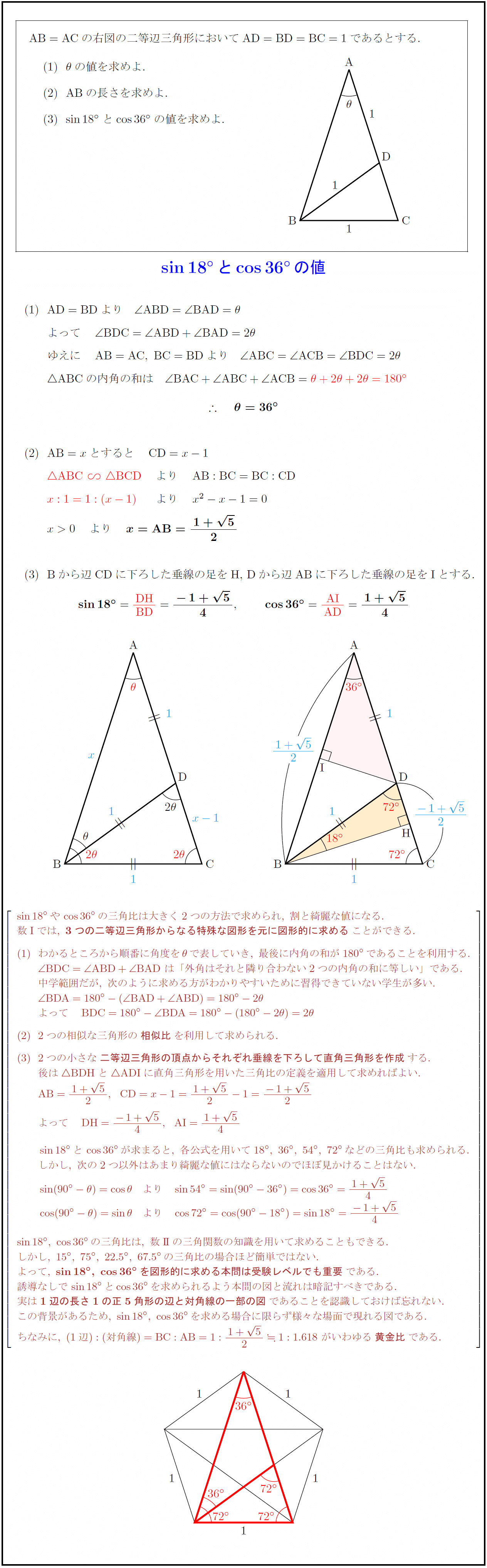
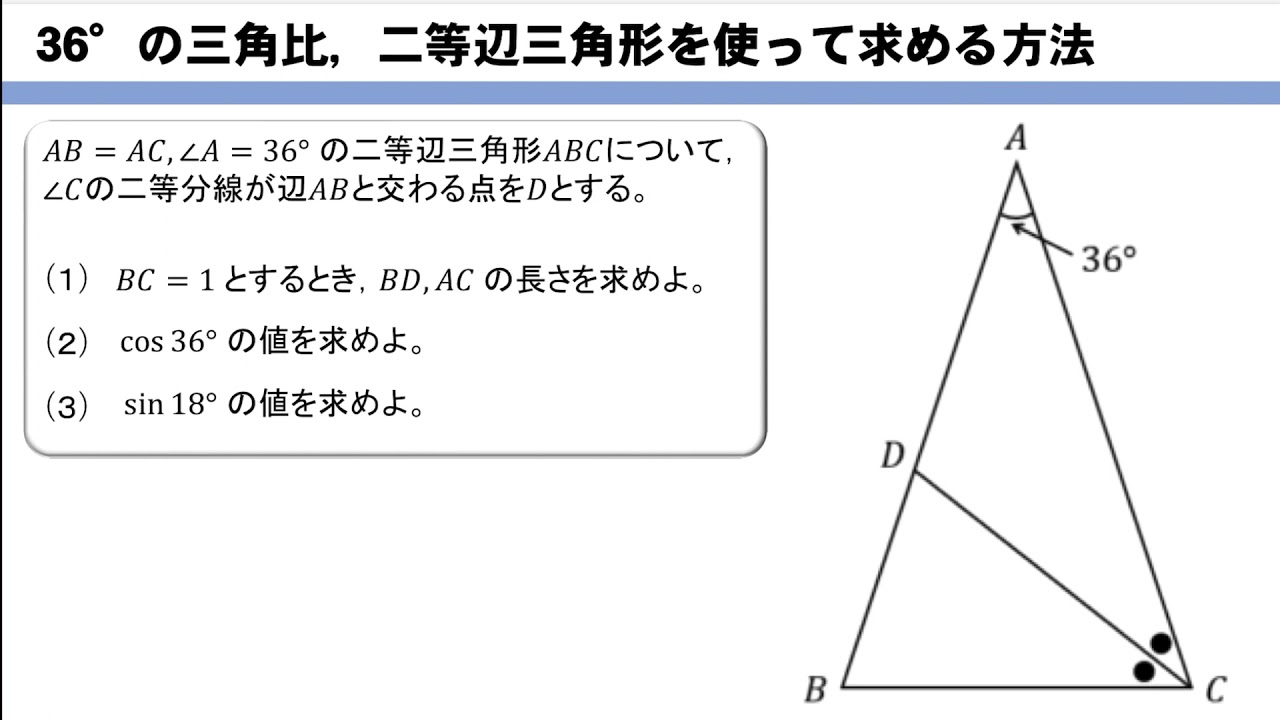
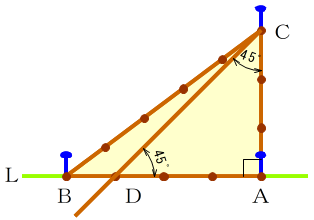
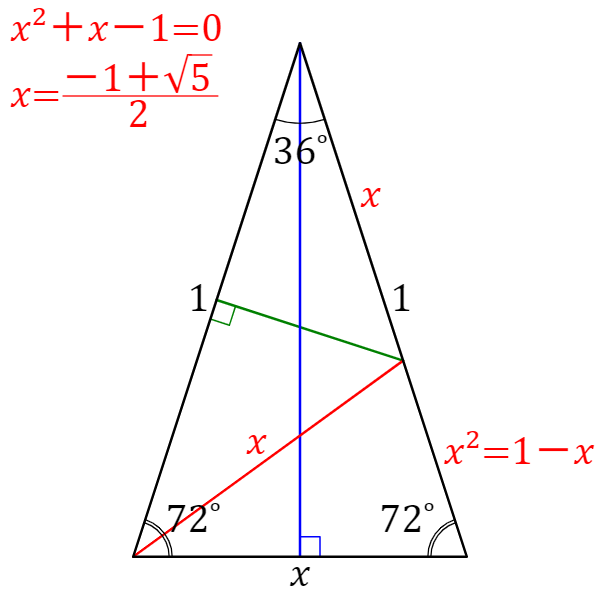
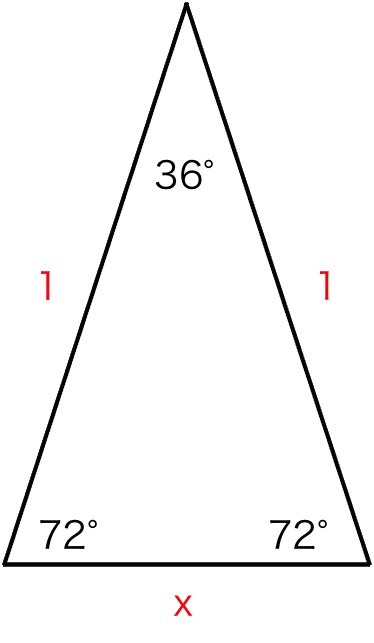
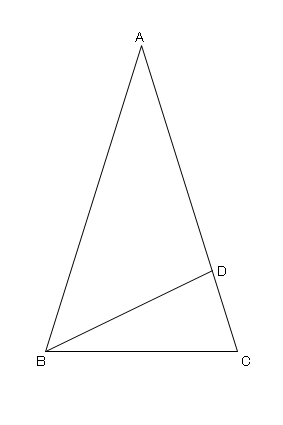
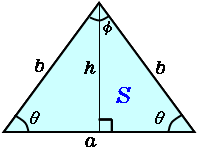
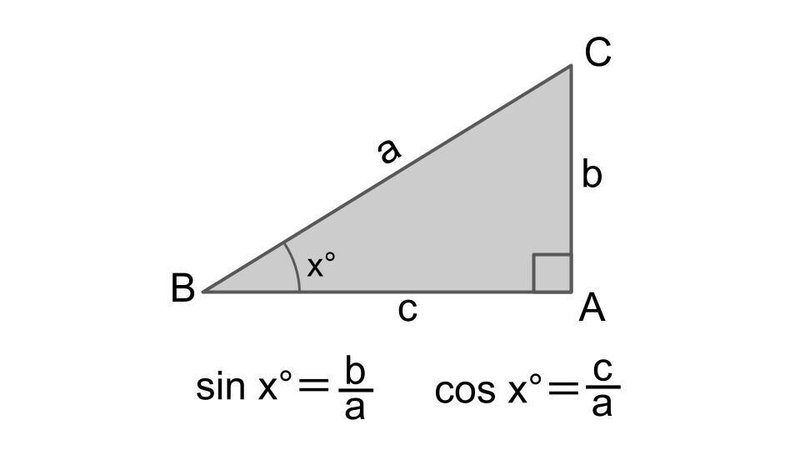
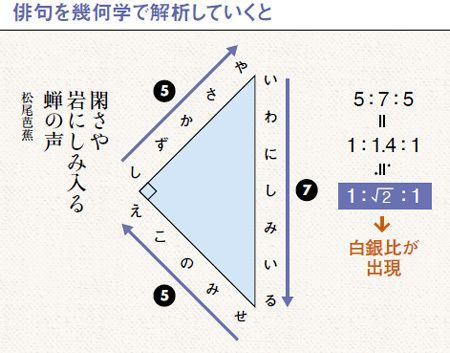
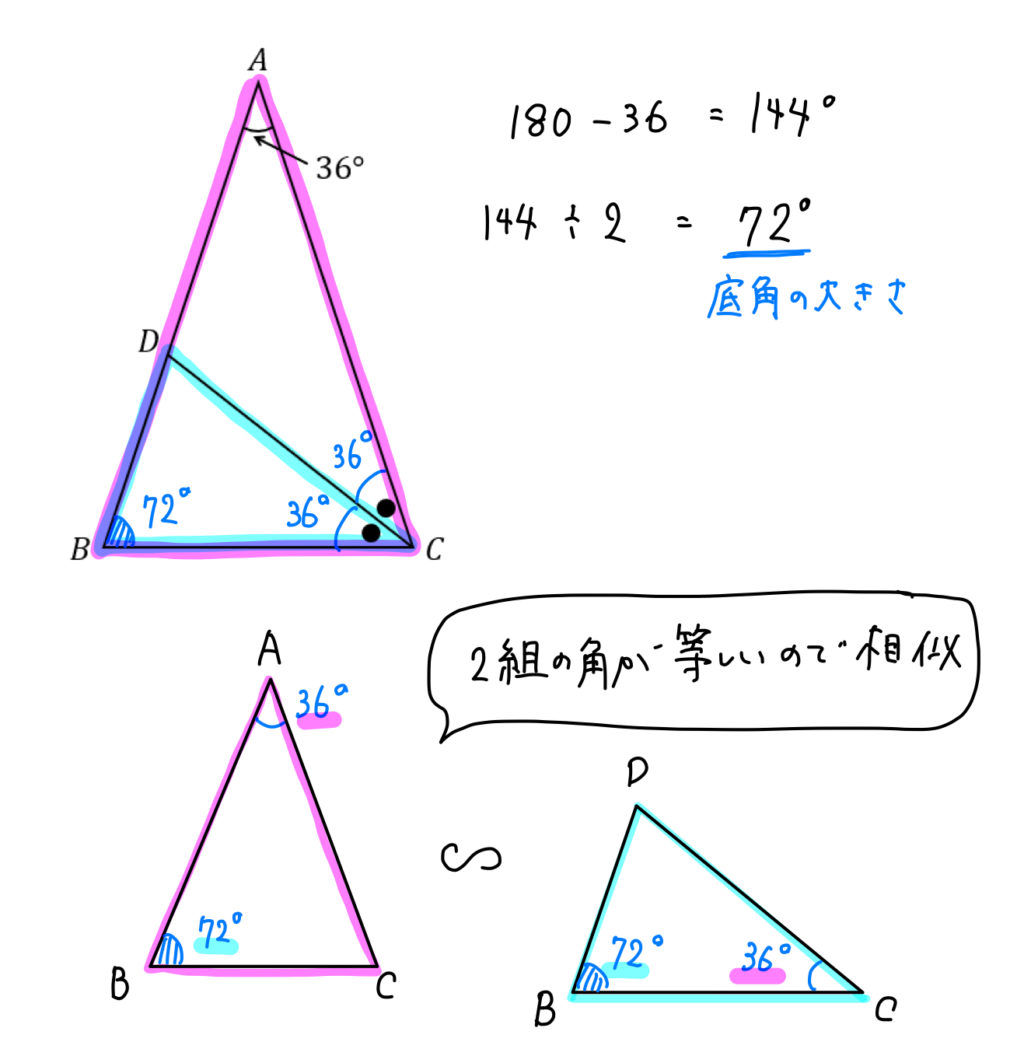
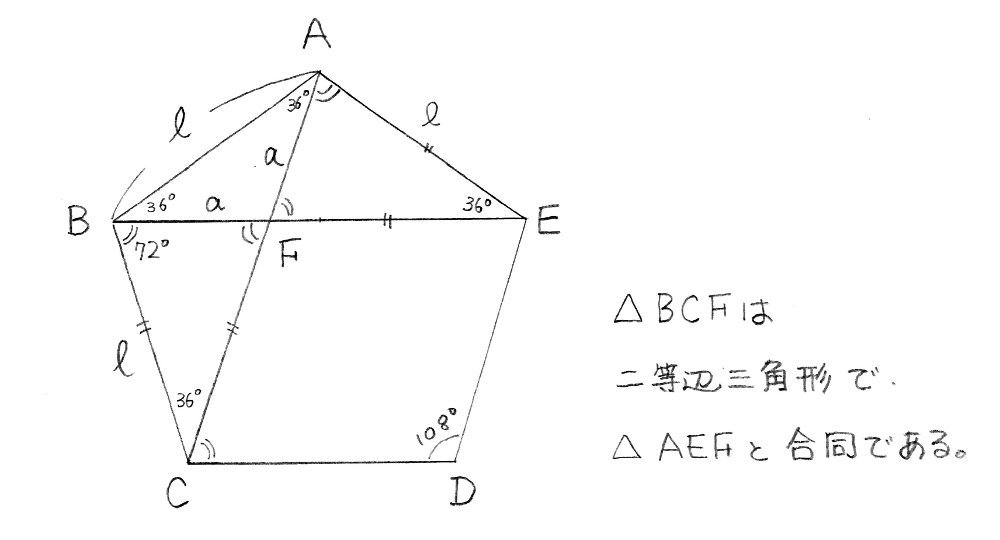
それぞれの辺の比は二等辺三角形・正三角形の性質から導けますが、よく利用することになるので覚えておきましょう。 30°、60°、90°の直角三角形→辺の長さの比は\(1:2:\sqrt{3}\) 三角形の辺の長さの比が\(1:2:\sqrt{3}\)→ 30°、60°、90°の直角三角形さて,36度の三角比を求めるには,この形の中の acdを使う. つまり頂角36度,底角72度の二等辺三角形である. まず底角cの2等分線を引く.(正5角形の対角線ceにあたる) その線とadとの交点をqとすると, qacはa=c=36度の二等辺三角形である.





0 件のコメント:
コメントを投稿